Public Key Cryptography
This note is partly based on Section 1.4 of “Algorithms," by S. Dasgupta, C. Papadimitriou, and U. Vazirani, McGraw-Hill, 2007.
Public Key Cryptography
In this note, we discuss a very nice and important application of modular arithmetic: the RSA public-key cryptosystem, named after its inventors Ronald Rivest, Adi Shamir, and Leonard Adleman.
Cryptography is an ancient subject that really blossomed into its modern form at the same time1 as the other great revolutions in the general fields of information science/engineering. The setting for basic cryptography is typically described via a cast of three characters: Alice and Bob, who with to communicate confidentially over some (insecure) link, and Eve, an eavesdropper who is listening in and trying to discover what they are saying.
Let’s assume that Alice wants to transmit a message \(x\) (written in binary) to Bob. She will apply her encryption function \(E\) to \(x\) and send the encrypted message \(E(x)\) (also called the cyphertext) over the link; Bob, upon receipt of \(E(x)\), will then apply his decryption function \(D\) to it and thus recover the original message (also called the plaintext): i.e., \(D(E(x)) = x\).
Since the link is insecure, Alice and Bob have to assume that Eve may get hold of \(E(x)\). (Think of Eve as being a “sniffer" on the network.) Thus ideally we would like to know that the encryption function \(E\) is chosen so that just knowing \(E(x)\) (without knowing the decryption function \(D\)) doesn’t allow one to discover anything about the original message \(x\).
For millenia cryptography was based on what are now called private-key protocols. In such a scheme, Alice and Bob meet beforehand and together choose a secret codebook, with which they encrypt all future correspondence between them. (This codebook plays the role of the functions \(E\) and \(D\) above.) Eve’s only hope then is to collect some encrypted messages and use them to at least partially figure out the codebook.
Public-key schemes, such as RSA, are significantly more subtle and tricky: they allow Alice to send Bob a secure message without ever having met him privately before! This almost sounds impossible, because in this scenario there is a symmetry between Bob and Eve: why should Bob have any advantage over Eve in terms of being able to understand Alice’s message? The central idea between the RSA cryptosystem is that Bob is able to implement a digital lock, to which only he has the key. Now by making this digital lock public, he gives Alice (or, indeed, anybody else) a way to send him a secure message which only he can open.
Here is how the digital lock is implemented in the RSA scheme. Each person has a public key known to the whole world, and a private key known only to themselves. When Alice wants to send a message \(x\) to Bob, she encodes it using Bob’s public key. Bob then decrypts it using his private key, thus retrieving \(x\). Eve is welcome to see as many encrypted messages for Bob as she likes, but she will not be able to decode them (under certain simple assumptions explained below).
But before we can go into how to use modulo arithmetic to achieve this sort of scheme, we need to review some basic properties of functions.
Bijections
A function is a mapping from a set (called the domain) of inputs \(A\) to a set of outputs \(B\): for input \(x\in A\), \(f(x)\) must be in the set \(B\). To denote such a function, we write \(f: A\rightarrow B\). The set \(B\) is known as the codomain of \(f\), but it is important to recognize that \(f\) may not output every element in \(B\). For example, we write \(f : {\mathbb{R}}\to {\mathbb{R}}\) for the function \(f(x) := x^2\), but the function \(f\) only ever outputs non-negative numbers. To distinguish between the set \(B\) and the actual possible outputs of \(f\), we define the set \(f(A) := \{f(a) : a \in A\}\) to be the range (or image) of \(f\). In the example of \(f(x) = x^2\), the range is the set of non-negative real numbers.
Consider the following examples of functions, where both functions map \(\{0,\dots,m-1\}\) to itself: \[f(x) = x + 1 \bmod m\] \[g(x) = 2x \bmod m\]
A bijection is a function for which every \(b\in B\) has a unique pre-image \(a\in A\) such that \(f(a) = b\). Note that this consists of two conditions:
\(f\) is onto: every \(b \in B\) has a pre-image \(a\in A\).
\(f\) is one-to-one: for all \(a,a'\in A\), if \(f(a) = f(a')\) then \(a = a'\).
Looking back at our examples, we can see that \(f\) is a bijection; the unique pre-image of \(y\) is \(y - 1\). However, \(g\) is only a bijection if \(m\) is odd. Otherwise, it is neither one-to-one nor onto. The following lemma can be used to prove that a function is a bijection:
Lemma 1
For a finite set \(A\), \(f: A\rightarrow A\) is a bijection if there is an inverse function \(g: A\rightarrow A\) such that \(\forall x\in A\) \(g(f(x)) = x\).
Proof. If \(f(x) = f(x')\), then \(x = g(f(x)) = g(f(x')) = x'\). Therefore, \(f\) is one-to-one. Since \(f\) is one-to-one, there must be \(|A|\) elements in the range of \(f\). This implies that \(f\) is also onto. \(\square\)
Moreover, in the case that \(f\) maps a finite set to itself, if \(f\) to be one-to-one then it is necessarily onto:
Lemma 2
If \(f:A \rightarrow A\) is one-to-one and \(A\) is a finite set, then \(f\) is a bijection.
Proof. Let \(|A| = n\). Since \(f\) is one-to-one, there must be \(n\) elements in the image of \(f\). But that means that every element in \(A\) must be hit. \(\square\)
RSA
A particularly practical family of bijections is the RSA function, named after its inventors Ronald Rivest, Adi Shamir, and Leonard Adleman:
\[E(x) = x^e \bmod N\]
where \(N= pq\) (\(p\) and \(q\) are two large primes), \(E: \{0,\dots,N-1\}\rightarrow\{0,\dots,N-1\}\) and \(e\) is relatively prime to \((p-1)(q-1)\). The inverse of the RSA function is:
\[D(x) = x^d \bmod N\]
where \(d\) is the inverse of \(e \mod (p-1)(q-1)\). In other words \(ed \equiv 1 \pmod{(p-1)(q-1)}\).
Let’s bring back our standard cast of characters and assume that Alice wants to transmit a message \(x\) (mapped into a number between \(2\) and \(N - 1\). Can you see why we avoid both \(0\) and \(1\)?) to Bob. In order to encrypt the message, Alice only needs Bob’s public key \((N,e)\). In order to decrypt the message, Bob needs his private key \(d\). The pair \((N,e)\) can be thought of as the serial number of the public lock - anyone can place a message in a box and lock it, but only Bob has the key \(d\) to open the lock. The idea is that since Eve does not have access to \(d\), she will not be able to gain information about Alice’s message.
Here is an example:
Example: Let \(p=5\), \(q=11\), and \(N=pq=55\). (In practice, \(p\) and \(q\) would be much larger.) Then we can choose \(e=3\), which is relatively prime to \((p-1)(q-1)=40\). Thus Bob’s public key is \((55,3)\). His private key is \(d=3^{-1}\pmod{40} = 27\). For any message \(x\) that Alice (or anybody else) wishes to send to Bob, the encryption of \(x\) is \(y = x^3\bmod 55\), and the decryption of \(y\) is \(x=y^{27}\bmod 55\). So, for example, if the message is \(x=13\), then the encryption is \(y=13^3=52\bmod 55\), and this is decrypted as \(13=52^{27}\bmod 55\).
We will now prove that \(D(E(x)) = x\) (and therefore \(E(x)\) is a bijection). We will require a beautiful theorem from number theory known as Fermat’s Little Theorem, which is the following:
Theorem 1 (Fermat's Little Theorem)
For any prime \(p\) and any \(a\in\{1,2,\ldots,p-1\}\), we have \(a^{p-1} \equiv 1 \pmod{p}\).
Let \(S\) be the nonzero integers modulo \(p\); that is, \(S = \{1,2,\ldots, p-1\}\). Define a function \(f: S\rightarrow S\) such that \(f(x) = ax\bmod p\). Here’s the crucial observation: \(f\) is simply a bijection from \(S\) to \(S\); it permutes the elements of \(S\). For instance, here’s a picture of the case \(a = 3, p = 7\):
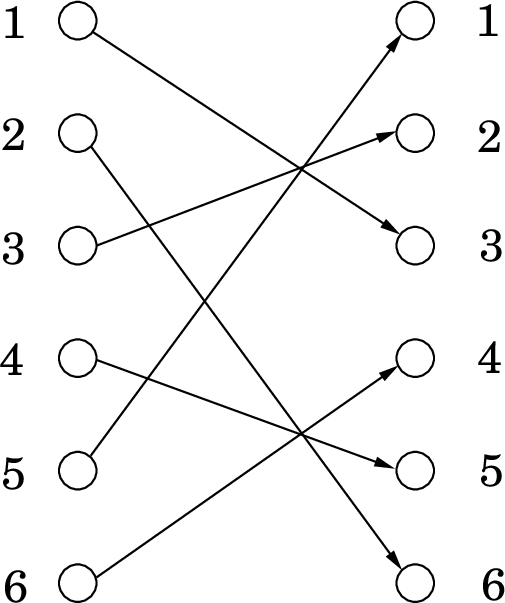
Figure 1: Multiplication by \(3\), mod \(7\).
With this intuition, we can now prove Fermat’s Little Theorem:
Proof of Theorem 1. Our first claim is that \(f(x)\) is a bijection. We will then show that this claim implies the theorem.
To show that \(f\) is a bijection, we simply need to argue that the numbers \(a\cdot i\bmod p\) are distinct. This is because if \(a \cdot i \equiv a \cdot j \pmod p\), then dividing both sides by \(a\) gives \(i \equiv j \pmod p\). They are nonzero because \(a \cdot i \equiv 0\) similarly implies \(i \equiv 0\). (And we can divide by \(a\), because by assumption it is nonzero and therefore relatively prime to \(p\). So a multiplicative inverse for \(a\) must exist.)
Now we can prove the theorem. Since \(f\) is a bijection, we know that the image of \(f\) is \(S\). Now if we take the product of all elements in \(S\), it is equal to the product of all elements in the image of \(f\). We are essentially looping through the elements of \(S\) in two different ways2. Once in their natural order, and then again in the permuted ordering defined by \(f\). So \[(p-1)! \equiv a^{p-1} \cdot (p-1)! \pmod p .\] Dividing both sides by \((p-1)!\) (which we can do because it is relatively prime to \(p\), since \(p\) is assumed prime) then gives the theorem. \(\square\)
Let us return to proving that \(D(E(x)) = x\):
Theorem 2
Under the above definitions of the encryption and decryption functions \(E\) and \(D\), we have \(D(E(x)) = x\bmod N\) for every possible message \(x\in\{0,1,\ldots,N-1\}\).
The proof of this theorem relies on Fermat’s Little Theorem:
Proof of Theorem 2. To prove the statement, we have to show that \[ (x^e)^d = x\bmod N\qquad\text{for every $x\in\{0,1,\ldots,N-1\}$}.\](1) Let’s consider the exponent, which is \(ed\). By definition of \(d\), we know that \(ed=1\bmod (p-1)(q-1)\); hence we can write \(ed = 1+k(p-1)(q-1)\) for some integer \(k\), and therefore \[ x^{ed} - x = x^{1+k(p-1)(q-1)} - x = x(x^{k(p-1)(q-1)}-1).\](2) Looking back at Equation 1, our goal is to show that this last expression in Equation 2 is equal to \(0\) mod \(N\) for every \(x\).
Now we claim that the expression \(x(x^{k(p-1)(q-1)}-1)\) in Equation 2 is divisible by \(p\). To see this, we consider two cases:
Case 1. \(x\) is not a multiple of \(p\). In this case, since \(x\ne 0\bmod p\), we can use Fermat’s Little Theorem to deduce that \(x^{p-1}=1\bmod p\). Then \((x^{p-1})^{k(q-1)}\equiv 1^{k(q-1)}\bmod p\) and hence \(x^{k(p-1)(q-1)}-1=0\bmod p\), as required.
Case 2. \(x\) is a multiple of \(p\). In this case the expression in Equation 2, which has \(x\) as a factor, is clearly divisible by \(p\).
By an entirely symmetrical argument, \(x(x^{k(p-1)(q-1)}-1)\) is also divisible by \(q\). Therefore, it is divisible by both \(p\) and \(q\), and since \(p\) and \(q\) are primes it must be divisible by their product, \(pq=N\). But this implies that the expression is equal to 0 mod \(N\), which is exactly what we wanted to prove. \(\square\)
[Encryption]: When Alice wants to send a message \(x\) (assumed to be an integer mod \(N\)) to Bob, she computes the value \(E(x)\), which is itself an integer mod \(N\), and sends this to Bob.
[Decryption]: Upon receiving the value \(y=E(x)\), Bob computes \(D(y)\), and this is equal to the original message \(x\).
Let us understand the properties that the encryption and decryption functions \(E\) and \(D\) must satisfy for these conditions to hold.
So we have seen that the RSA protocol is correct, in the sense that Alice can encrypt messages in such a way that Bob can reliably decrypt them again. But how do we know that it is secure, i.e., that Eve cannot get any useful information by observing the encrypted messages? The security of RSA hinges upon the following simple assumption: \[\text{Given $N$, $e$ and $y=x^e\bmod N$, there is no efficient algorithm for determining $x$.}\] This assumption is quite plausible. How might Eve try to guess \(x\)? She could experiment with all possible values of \(x\), each time checking whether \(x^e=y\bmod N\); but she would have to try on the order of \(N\) values of \(x\), which is completely unrealistic if \(N\) is a number with (say) \(512\) bits. This is because \(N \approx 2^{512}\) is larger than estimates for the age of the Universe in femtoseconds! Alternatively, she could try to factor \(N\) to retrieve \(p\) and \(q\), and then figure out \(d\) by computing the inverse of \(e\) mod \((p-1)(q-1)\); but this approach requires Eve to be able to factor \(N\) into its prime factors, a problem which is believed to be impossible to solve efficiently for large values of \(N\). She could try to compute the quantity \((p-1)(q-1)\) without factoring \(N\); but it is possible to show that computing \((p-1)(q-1)\) is equivalent to factoring \(N\). We should point out that the security of RSA has not been formally proved: it rests on the assumptions that breaking RSA is essentially tantamount to factoring \(N\), and that factoring is hard.
We close this note with a brief discussion of implementation issues for RSA. Since we have argued that breaking RSA is impossible because factoring would take a very long time, we should check that the computations that Alice and Bob themselves have to perform are much simpler, and can be done efficiently.
There are really only two non-trivial things that Alice and Bob have to do:
Bob has to find prime numbers \(p\) and \(q\), each having many (say, \(512\)) bits.
Both Alice and Bob have to compute exponentials mod \(N\). (Alice has to compute \(x^e\bmod N\), and Bob has to compute \(y^d\bmod N\).)
Both of these tasks can be carried out efficiently. The first requires a rich source of primes3. You will learn how to do this task in the upper-division algorithms course 170, and this is based on results from number theory. The second requires an efficient algorithm for modular exponentiation, which you have already seen in the previous note. You can further speed up the decryption step by leaning on the Chinese Remainder Theorem and working in coordinates mod \(p\) and mod \(q\).
To summarize, then, in the RSA protocol Bob need only perform simple calculations such as multiplication, exponentiation and primality testing to implement his digital lock. Similarly, Alice and Bob need only perform simple calculations to lock and unlock the the message respectively—operations that any pocket computing device could handle. By contrast, to unlock the message without the key, Eve would have to perform operations like factoring large numbers, which (at least according to widely accepted belief) requires more computational power than all the world’s most sophisticated computers combined! This compelling guarantee of security without the need for private keys explains why the RSA cryptosystem is such a revolutionary development in cryptography.
And in reality, involving some of the same cast of characters. Both Alan Turing and Claude Shannon were active in codebreaking during the war and Shannon had a classic paper that is considered the birth of the information-theoretic understanding of secrecy and dovetails with his other more famous paper that gave rise to the modern information-theoretic view of communication. Both cryptography and communication weave together information, computation, and randomness in surprising ways. In 70, you just get a tiny taste of these spectacularly beautiful fields.↩
This sort of thing is something that we will be doing often in this course — looking at the same thing in two different ways.↩
To find large prime numbers, we use the fact that, given a positive integer \(n\), there is an efficient algorithm that determines whether or not \(n\) is prime. (Here “efficient" means a running time of \(O((\log n)^k)\) for some small \(k\), i.e., a low-degree power of the number of bits in \(n\). Notice the dramatic contrast here with factoring: we can tell efficiently whether or not \(n\) is prime, but in the case that it is not prime we cannot efficiently find its factors. The success of RSA hinges crucially on this distinction.) Given that we can test for primes, Bob just needs to generate some random integers \(n\) with the right number of bits, and test them until he finds two primes \(p\) and \(q\). This works because of the following basic fact from number theory (which we will not prove), which says that a reasonably large fraction of positive integers are prime:
Theorem 3 (Prime Number Theorem)
Let \(\pi(n)\) denote the number of primes that are less than or equal to \(n\). Then for all \(n\ge 17\), we have \[\pi(n)\ge\frac{n}{\ln n}.\] In fact, \[\lim_{n\to\infty}\frac{\pi(n)}{n/\ln n} = 1.\]
Setting \(n=2^{512}\), for example, the Prime Number Theorem says that roughly one in every \(355\) of all \(512\)-bit numbers are prime. Therefore, if we keep picking random \(512\)-bit numbers and testing them, we would expect to have to try only about \(355\) numbers until we find a prime.↩